Proper Coloring In Graph Theory, Exact Coloring Wikipedia

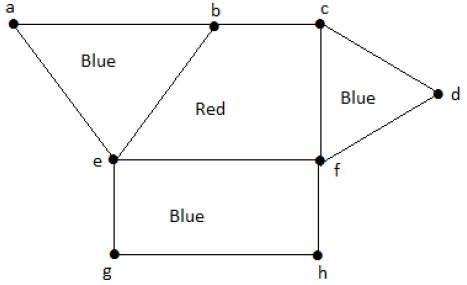
Usually we drop the word proper unless other types of coloring are also under discussion.

Name gabby coloring. The most common type of vertex coloring seeks to minimize the number of colors for a given graph. A graph g is a mathematical structure consisting of two sets vg vertices of g and eg edges of g. Such a coloring is known as a minimum vertex coloring and the minimum number of colors which with the vertices of a graph g may be colored is called the.

This is called a vertex coloringsimilarly an edge coloring assigns a color to each. Proper coloring of a graph is an assignment of colors either to the vertices of the graphs. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.

The most common type of edge coloring is analogous to graph vertex colorings. Definition 581 a proper coloring of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color. A graph g then g has a proper coloring with d1 or fewer colors ie the chromatic number of g is at most d1.

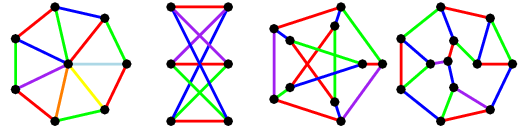
Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints. Browse other questions tagged graph theory self learning or ask your own question. For example the figure to the right shows an edge coloring of a graph by the colors red blue and green.

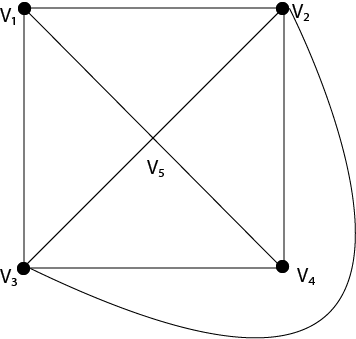
With cycle graphs the analogy becomes an equivalence as there is an edge. The smallest number of colors needed to get a proper vertex coloring is called the chromatic number of the graph written chig. In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors.

For example you could color every vertex with a different color. Such a coloring is a proper edge coloring. A proper edge coloring with 4 colors.

For example color the two vertical edges red the horizontal edges green and the diagonals blue. Each edge of a graph has a color assigned to it in such a way that no two adjacent edges are the same color. Find the chromatic number of the graphs below.

A vertex coloring is an assignment of labels or colors to each vertex of a graph such that no edge connects two identically colored vertices. In graph theory an edge coloring of a graph is an assignment of colors to the edges of the graph so that no two incident edges have the same color. This gives an upper bound on the chromatic number but the real chromatic number may be below this upper bound.

In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color. But often you can do better. Featured on meta new post formatting.

For example in our course con. In graph theory graph coloring is a special case of graph labeling. This graph has a proper edge coloring with 3 colors.