Graph Theory Coloring Problems, Vertex Coloring Martin Thoma

Given a graph gve with n vertices and m edges the aim is to color the vertices of.

Easter coloring sheets christian. Was introduced in order to solve the problem of coloring countries on a map so that no two countries that shared a border received the same color. That problem provided the original motivation for the development of algebraic graph theory and the study of graph invariants such as those discussed on this page. Graph coloring gcp is one of the most studied problems in both graph theory and combinatorial optimization.

So the minimum value of k for which such a. All right and then the minimum number of colors you need is called the chromatic number of the graph. Unfortunately there is no efficient algorithm available for coloring a graph with minimum number of colors as the problem is a known np complete problemthere are approximate algorithms to solve the problem though.

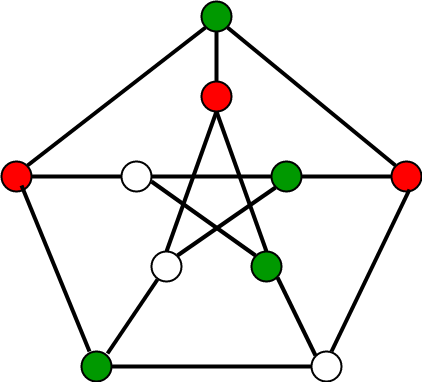
Now this is an example of whats called a graph coloring problem. Definition 581 a proper coloring of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color. This most basic variant of graph coloring known as a proper coloring is a key concept in modern graph theory.

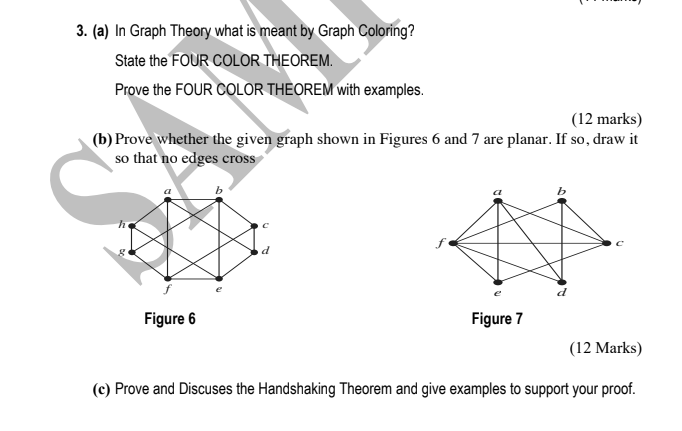
Given a graph g and k colors assign a color to each node so that adjacent nodes get different colors. Vertex coloring is the most common graph coloring problem. The study of graph colorings has historically been linked closely to that of planar graphs and the four color theorem which is also the most famous graph coloring problem.

Theory algorithms and applications by jorgen bang jensen and gregory gutin springer 2001 and 2008 is a comprehensive text on directed graphs containing material on the relations of graph orientations with coloring and integer flows and with discussion of directed graph homomorphisms among other topics. So lets define that. Coloring problems in graph theory kevin moss iowa state university follow this and additional works athttpslibdriastateeduetd part of thecomputer sciences commons and themathematics commons this dissertation is brought to you for free and open access by the iowa state university capstones theses and dissertations at iowa state university.

Indeed the cornerstone of the theory of proper graph colorings the four color theorem. The problem is given m colors find a way of coloring the vertices of a graph such that no two adjacent vertices are colored using same color. Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints.