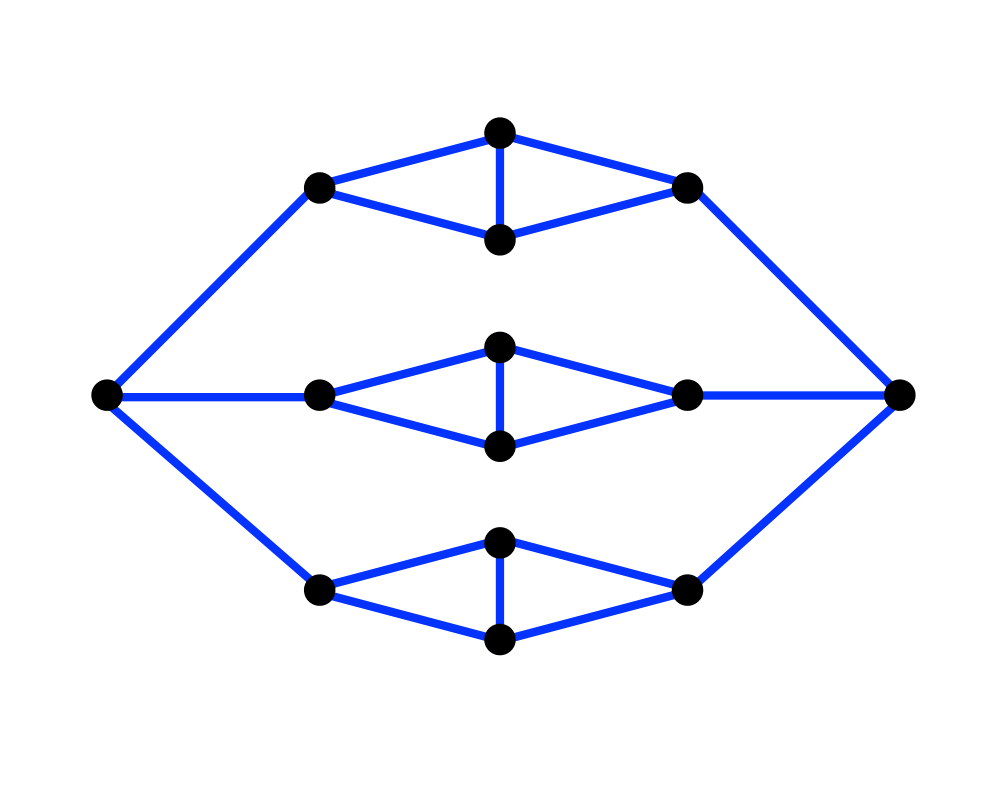
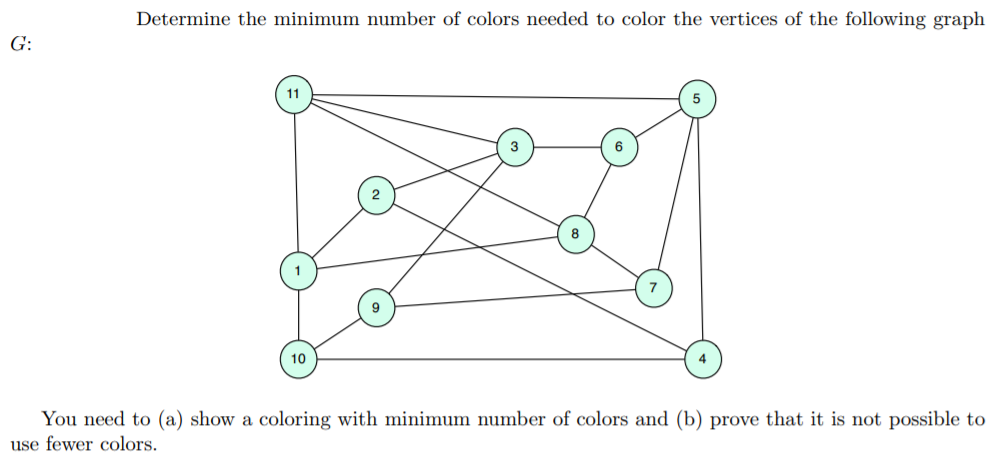
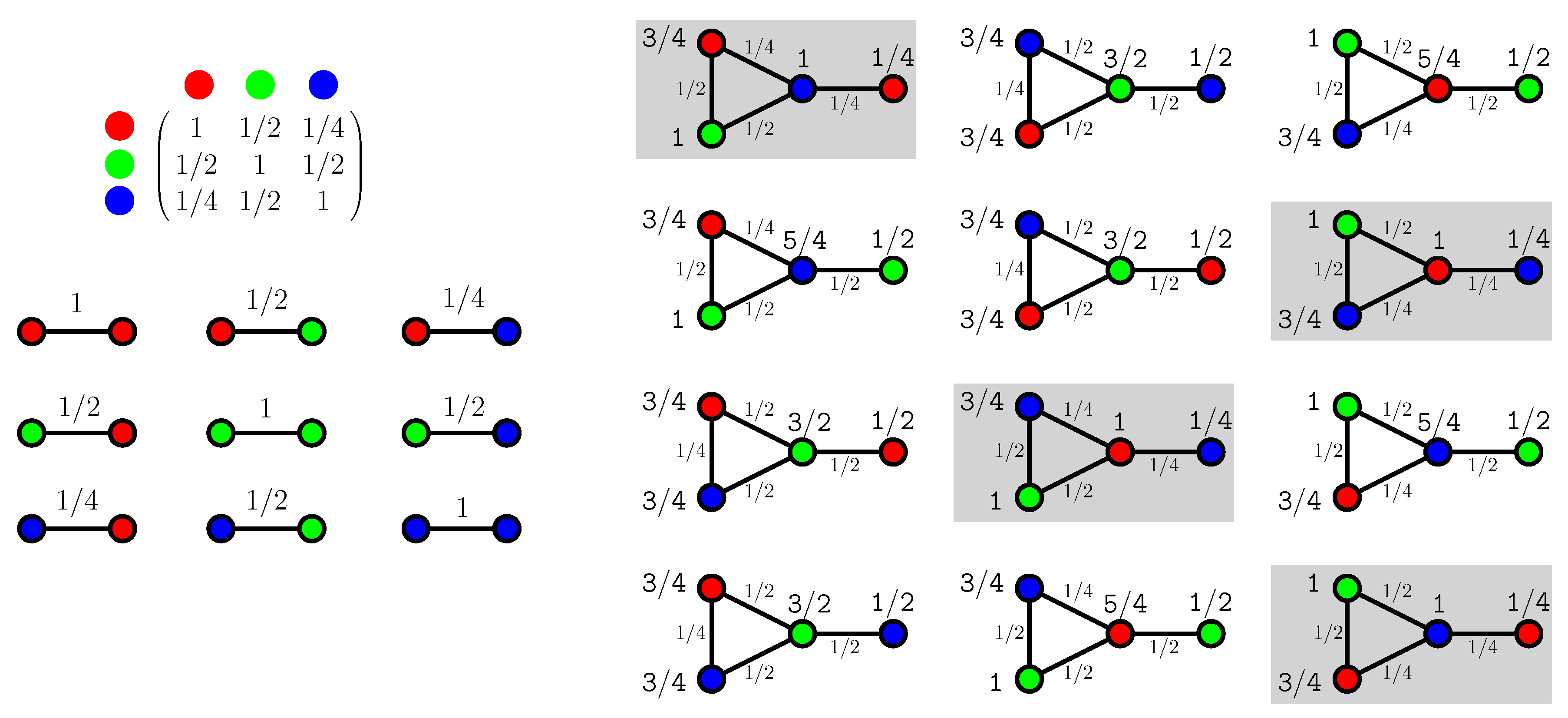
Graph Coloring Minimum Number Of Colors, Coloring
Graph coloring minimum number of colors Indeed lately has been sought by users around us, maybe one of you personally. People now are accustomed to using the net in gadgets to see video and image information for inspiration, and according to the name of the article I will talk about about Graph Coloring Minimum Number Of Colors.
- Graph Coloring Ppt Video Online Download
- Mathematician Disproves Hedetniemi S Graph Theory Conjecture Quanta Magazine
- Gate2004 77 Gate Overflow
- Programming Interview Graph Coloring Using Backtracking Youtube
- Coloring The Four Color Theorem
- 1 Graph Coloring Example 1 Graph Coloring Example Shows An Example Of Download Scientific Diagram
Find, Read, And Discover Graph Coloring Minimum Number Of Colors, Such Us:
- 12 Eng Equitable Coloring Of Prism G M Raja By Impact Journals Issuu
- Graph Coloring
- Graph Algorithm Tutorialspoint
- Graph Theory Unit Ppt Video Online Download
- Graph Coloring Minimum Number Of Colors Lovely Control Panel Wire Color Numbers Chart In 2020 Electrical Wiring Colours Electrical Wiring Color Coding
If you re looking for Bubble Letters Coloring Pages you've come to the right location. We ve got 104 graphics about bubble letters coloring pages adding images, photos, photographs, backgrounds, and much more. In such page, we additionally provide variety of graphics out there. Such as png, jpg, animated gifs, pic art, symbol, black and white, transparent, etc.
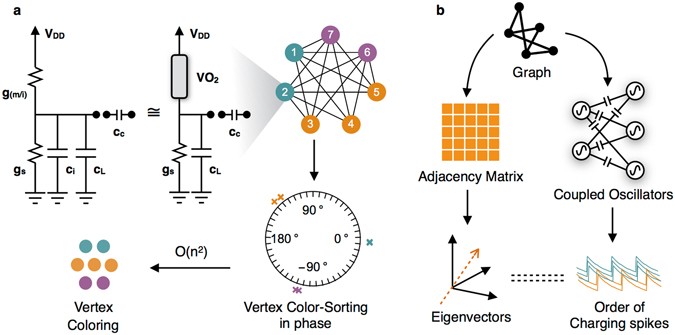
Vertex Coloring Of Graphs Via Phase Dynamics Of Coupled Oscillatory Networks Scientific Reports Bubble Letters Coloring Pages
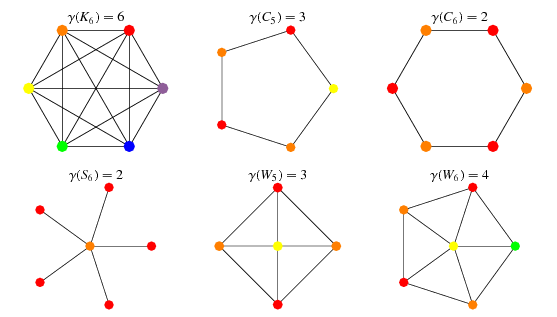
The smallest number of colors needed to color a graph g is called its chromatic number.
Bubble letters coloring pages. Precise formulation of the theorem. The other graph coloring problems like edge coloring no vertex is incident to two edges of same color and face coloring geographical map coloring can be transformed into vertex coloring. 24 valid colorings every assignment of four colors to any 4 vertex graph is a proper coloring.
So for the graph in the example a table of the number of valid. Unfortunately there is no efficient algorithm available for coloring a graph with minimum number of colors as the problem is a known np complete problemthere are approximate algorithms to solve the problem though. In graph theoretic terms the theorem states that for loopless planar graph the chromatic number of its dual graph is.
For example the following can be colored minimum. The minimum number of colors required for vertex coloring of graph g is called as the chromatic number of g denoted by xg. The intuitive statement of the four color theorem given any separation of a plane into contiguous regions the regions can be colored using at most four colors so that no two adjacent regions have the same color needs.
As discussed in the previous post graph coloring is widely used. Color first vertex with the first color. Graph coloring algorithm there exists no efficient algorithm for coloring a graph with minimum number of colors.
Here coloring of a graph means the assignment of colors to all vertices. Below is the implementation of the above approach. Chromatic number of a graph is the minimum number of colors required to properly color the graph.
A 2d array graphvv where v is the number of vertices in graph and graphvv is adjacency matrix representation of the graph. However a following greedy algorithm is known for finding the chromatic number of any given graph. If g is not a null graph then xg 2.
Using all four colors there are 4. The maximum element in colors array will give the minimum number of colors required to color the given graph. Graph coloring is a np complete problem.
A value graphij is 1 if there is a direct edge from i to j otherwise graphij is 0. And for every choice of three of the four colors there are 12 valid 3 colorings. In the study of graph coloring problems in mathematics and computer science a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color.
Xg 1 if and only if g is a null graph. We introduced graph coloring and applications in previous post. An integer m which is.
Greedy colorings can be found in linear time but they do not in general use the minimum number of.
More From Bubble Letters Coloring Pages
- Art Coloring Book Pdf
- Coloring Competition For Kindergarten
- Blue Food Coloring To Tone Orange Hair
- Crayola Toy Story Coloring Pages
- Fairy Silhouette Coloring Pages
Incoming Search Terms:
- Solved Determine The Minimum Number Of Colors Needed To C Chegg Com Fairy Silhouette Coloring Pages,
- Graph Coloring Fairy Silhouette Coloring Pages,
- Graph Coloring Problem Techie Delight Fairy Silhouette Coloring Pages,
- Graph Coloring Definition Gate Vidyalay Fairy Silhouette Coloring Pages,
- Graph Coloring Minimum Number Of Colors Unique Minecraft Color Codes In 2020 Homeschool Minecraft Minecraft School Minecraft Classroom Fairy Silhouette Coloring Pages,
- Gate2004 77 Gate Overflow Fairy Silhouette Coloring Pages,