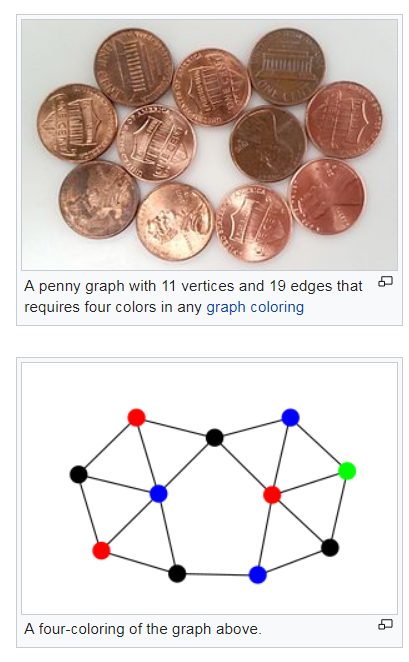
Coloring Number Of Planar Graphs, 1 Planar Graph Wikipedia

However for every k 3 a k coloring of a planar graph exists by the four color theorem and it is possible to find such a coloring in polynomial time.

Animal cell coloring page. An exact square coloring of a graph g is a vertex coloring in which any two vertices at distance exactly 2 receive distinct colors. This was finally proved in 1976 see figure 5103 with the aid of a computer. The best known approximation algorithm computes a coloring of size at most within a factor onlog log n 2 log n 3 of the chromatic number.

Region of a graph. 2017 an introduction to the discharging method via graph coloring. Two regions are said to be adjacent if they have a common edge.

Edges are colored in such a way that there does not exist a cycle of the same color and the minimal number of colors required for such an edge coloring of a given graph is known as its arboricity. Note a graph g is said to be n coverable if there is a vertex coloring that uses at most n colors ie xg n. In 1879 alfred kempe gave a proof that was widely known but was incorrect though it was not until 1890 that this was noticed by percy heawood who modified the proof to.

A graph is said to be planar if it can be drawn in a plane so that no edge cross. The number of colors needed to properly color any map is now the number of colors needed to color any planar graph. This problem was first posed in the nineteenth century and it was quickly conjectured that in all cases four colors suffice.

By vizings theorem the number of colors needed to edge color a simple graph is either its maximum degree d or d1. We apply the discharging method and the combinatorial nullstellensatz to show that every planar graph g with girth at least 5 has x s g 19 and for girth at least 6 7 and 26 x s g is at most 9 8 and 3 respectively. We study the exact square chromatic number of subcubic planar graphs.

For some graphs such as bipartite graphs and high degree planar graphs the number of colors is always d and for multigraphs the number of colors may be as large as 3d2. Consider a planar graph gvea region is defined to be an area of the plane that is bounded by edges and cannot be further subdivided. Journal of graph theory 85 4 721 737.

Prove that any planar graph has an edge coloring of at most three colors in which adjacent edges of the same color are allowed but cycles of edges of the same color are not. A planar graph divides the plans into one or more regions. Take a look at the following graph.

The graph shown in fig is planar graph. Region coloring is an assignment of colors to the regions of a planar graph such that no two adjacent regions have the same color. The smallest number of colors used in such a coloring of g is its exact square chromatic number denoted chisharp 2g.

In this paper we improve the current bounds on the additive coloring number for particular classes of graphs by proving results for a list version of additive coloring.