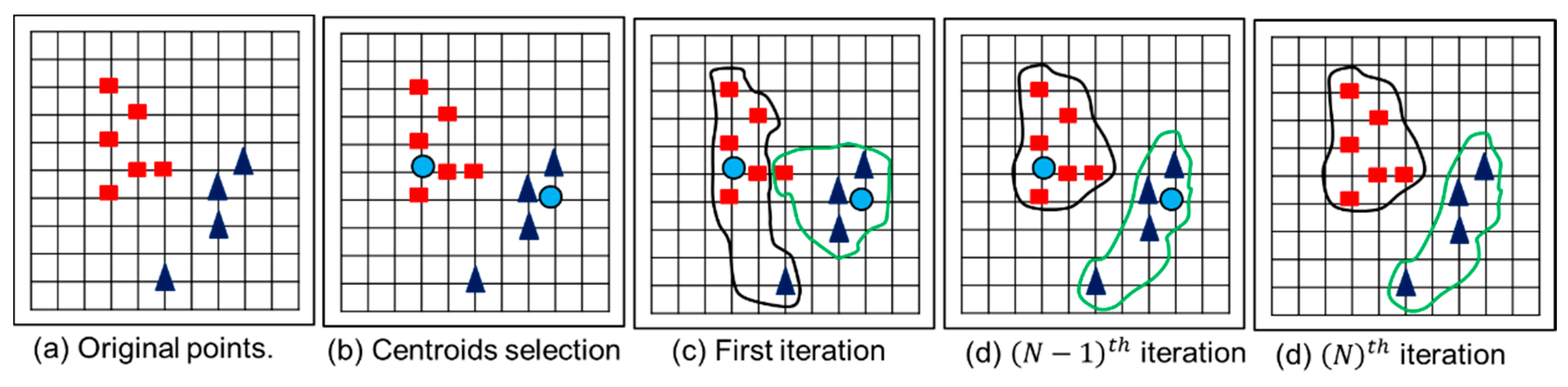
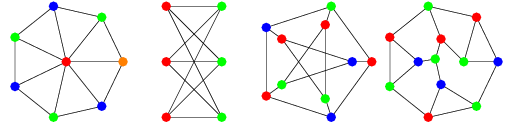
Coloring Algorithm Graph Theory, Overview Of Graph Colouring Algorithms

In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors.

Shark blaze coloring page. Isaacson the theory of graph coloring and relatively little study has been directed towards the design of efficient graph coloring procedures. Since numerous proofs of properties relevant to graph coloring are constructive many coloring procedures are at least implicit in the theoretical development. So lets define that and then see prove some facts about it.

And were going to call it the basic graph coloring algorithm. Introduction in graph theory graph coloring is a special case of graph labeling. In the program we have created the same graph as depicted in the first picture and successfully colored the graph using the backtracking algorithm.

It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. This is called a vertex coloring. The idea of coloring a graph is very straightforward and it seems as if it should be.

And that is probably the most basic graph coloring approach. Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraintsin its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color.

Unfortunately there is no efficient algorithm available for coloring a graph with minimum number of colors as the problem is a known np complete problemthere are approximate algorithms to solve the problem though. We introduced graph coloring and applications in previous post. This number is called the chromatic number and.

Graph coloring gcp is one of the most studied problems in both graph theory and combinatorial optimization. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color. 15 minutes coding time.

This project includes the implementation of various graph coloring algorithms. As discussed in the previous post graph coloring is widely used. Given a graph gve with n vertices and m edges the aim is to color the vertices of.

And almost you could almost say is a generic approach. This is called a vertex coloringsimilarly an edge coloring assigns a color to each. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.

A simple algorithm for graph coloring is easy to describe but potentially extremely expensive to run. In graph theory graph coloring is a special case of graph labeling. For backtracking we are returning false to rerun last recursive call to change the color of the last colored vertexif false is returned by the starting vertex then it means there is no solution.