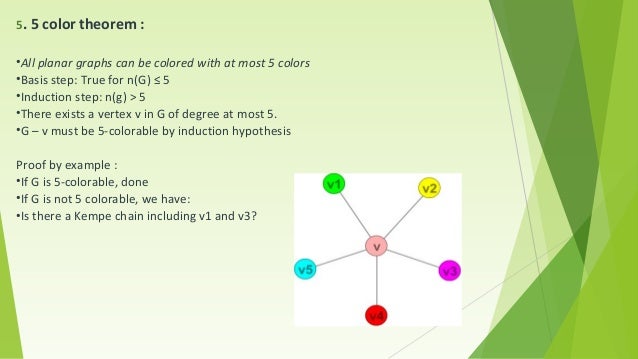
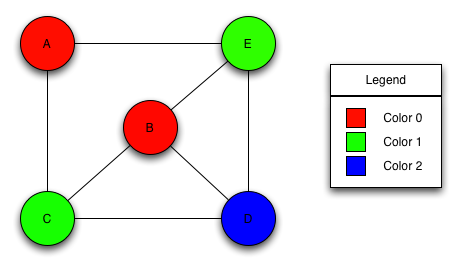
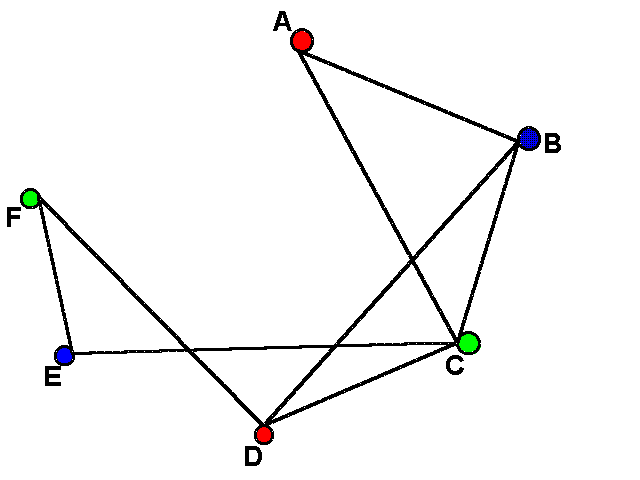
Vertex Coloring Number, Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins

This site is related to the classical vertex coloring problem in graph theory.

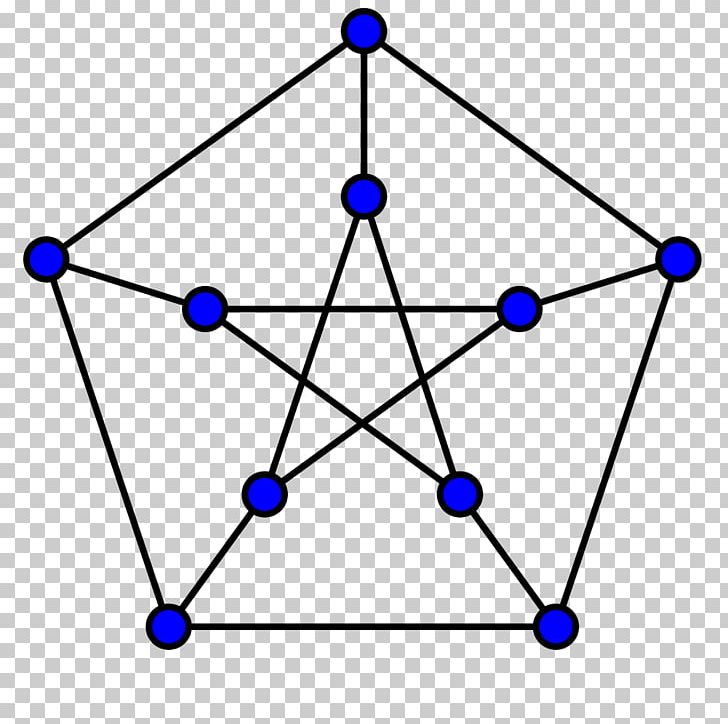
Valentine religious coloring pages. Zero knowledge protocol vertex coloring is relevant for so called zero knowledge protocols. Simply put no two vertices of an edge should be of the same color. Every graph has a proper vertex coloring.

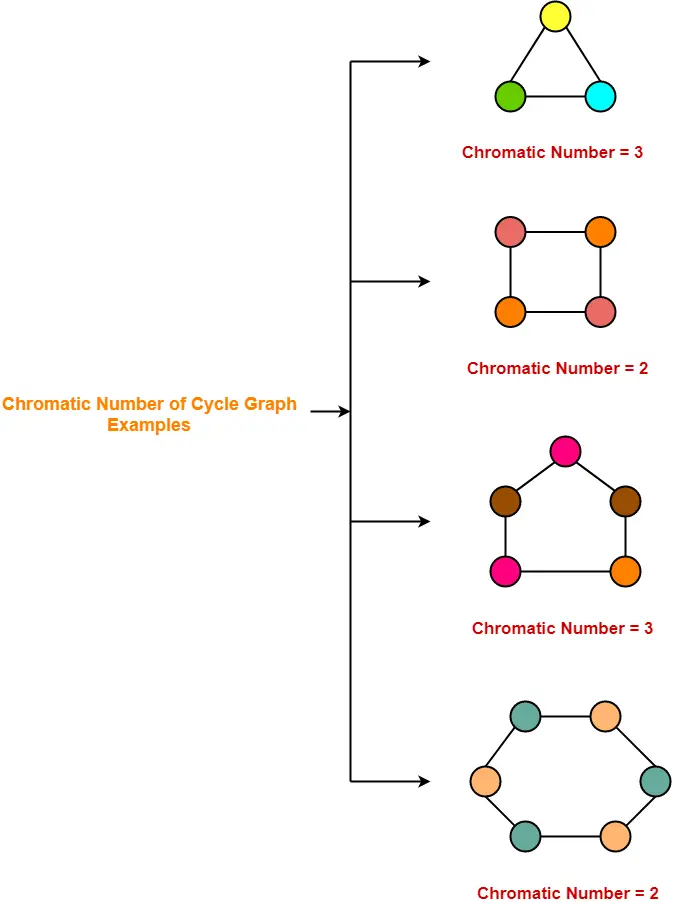
This is what we recognize as vertex colouring. If the vertex coloring has the property that adjacent vertices are colored differently then the coloring is called proper. The minimum number of colors required for vertex coloring of graph g is called as the chromatic number.

See the wikipedia article graphcoloring for further details on graph coloring. Used to count the possible number of ways of properly vertex coloring a graph. But often you can do better.

Vertex colouring and chromatic numbers. Imagine that we could take the vertices of a graph and colour or label them such that the vertices of any edge are coloured or labelled differently. Brelazs heuristic algorithm can be used to find a good but not necessarily.

Vertex coloring is an assignment of colors to the vertices of a graph g such that no two adjacent vertices have the same color. We present a new polynomial time algorithm for finding proper m colorings of the vertices of a graphwe prove that every graph with nvertices and maximum vertex degree i must have chromatic number ig less than or equal to i1 and that the algorithm will always find a proper m coloring of the vertices of gwith mless than or equal to i1. Graph coloring benchmarks instances and software.

As soon as you dont get valid colorings you know that the number of colors youve used in the last valid coloring was the minimum number. This function can compute the chromatic number of the given graph or test its k colorability. The minimum number of colors itself is called the chromatic number denoted and a graph with chromatic number is said to be a k chromatic graph.

P3 can be colored in 12 ways using 3 colors. The smallest number of colors needed to get a proper vertex coloring is called the. An edge coloring of a graph is a proper coloring of the edges meaning an assignment of colors to edges so that no vertex is incident to two edges of the same coloran edge coloring with k colors is called a k edge coloring and is equivalent to the problem of partitioning the edge set into k matchingsthe smallest number of colors needed for an edge coloring of a graph g is the chromatic index.

It presents a number of instances with best known lower bounds and upper bounds. For the same graphs are given also the best known bounds on the clique number. For example you could color every vertex with a different color.