Theory Of Graph Coloring Problem, Graph Theory Sample Exam I

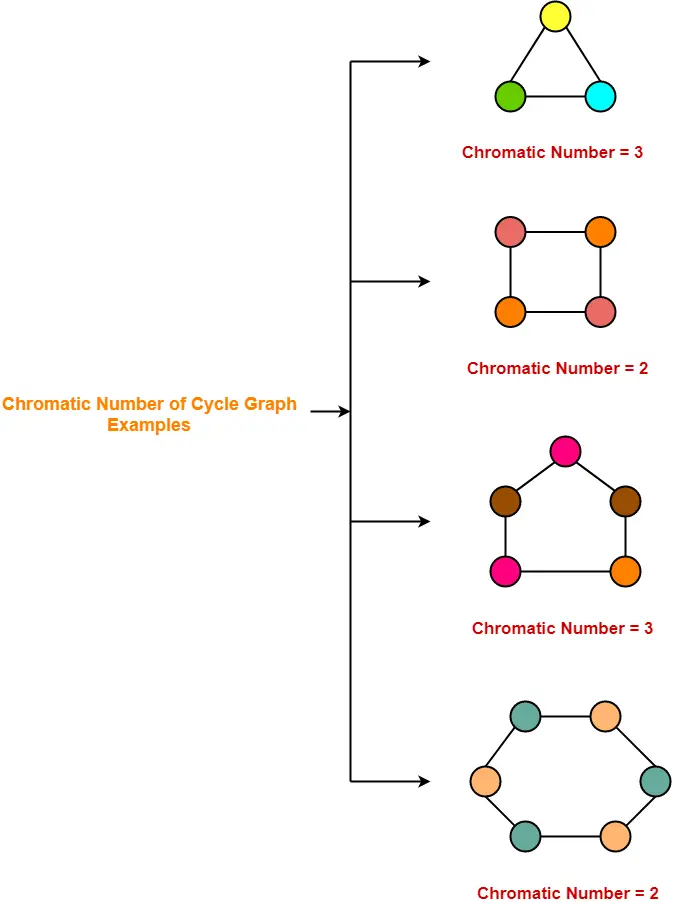
Introduction the origin of graph theory started with the problem of koinsber bridge in 1735.

Giant sticker animal coloring book. The intuitive statement of the four color theorem given any separation of a plane into contiguous regions the regions can be colored using at most four colors so that no two adjacent regions have the same color needs. In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors. Coloring problems in graph theory kevin moss iowa state university follow this and additional works athttpslibdriastateeduetd part of thecomputer sciences commons and themathematics commons this dissertation is brought to you for free and open access by the iowa state university capstones theses and dissertations at iowa state university.

So the minimum value of k for which such a. Here coloring of a graph means the assignment of colors to all vertices. This problem lead to the concept of eulerian graph.

This is called a vertex coloringsimilarly an edge coloring assigns a color to each. In graph theoretic terms the theorem states that for loopless planar graph the chromatic number of its dual graph is. It is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color.

It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. In graph theory graph coloring is a special case of graph labeling. Theory algorithms and applications by jorgen bang jensen and gregory gutin springer 2001 and 2008 is a comprehensive text on directed graphs containing material on the relations of graph orientations with coloring and integer flows and with discussion of directed graph homomorphisms among other topics.

Euler studied the problem of koinsberg bridge and constructed a structure to solve the problem called. Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints. Given a graph g and k colors assign a color to each node so that adjacent nodes get different colors.

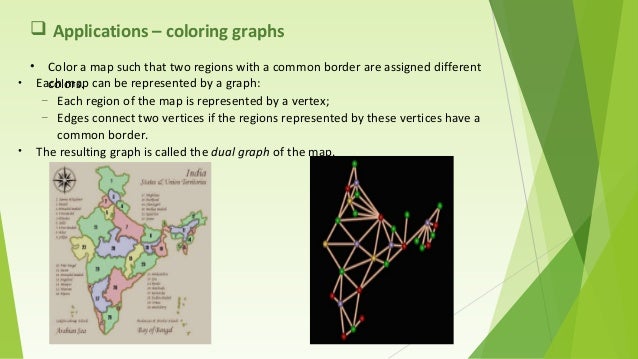
Timetabling and grouping problems scheduling problems graph coloring applications. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color.

A vertex coloring of a graph g is a mapping c. Vg s the elements of s are called colors. The vertices of one color form a color class.

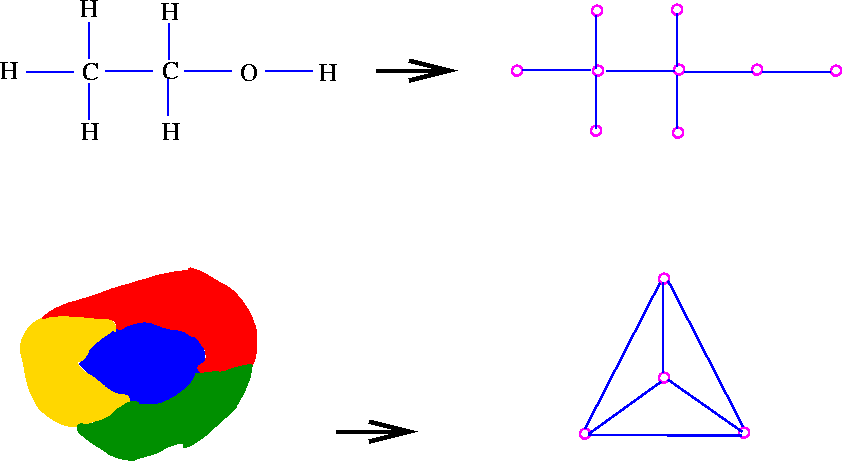
Now this is an example of whats called a graph coloring problem.