Graph Theory For Coloring, The Four Color Theorem
Graph theory for coloring Indeed lately is being sought by users around us, perhaps one of you personally. People are now accustomed to using the internet in gadgets to see image and video information for inspiration, and according to the name of this article I will discuss about Graph Theory For Coloring.
- Algorithmic Graph Theory Vertex Coloring Hu Berlin
- Decades Old Graph Problem Yields To Amateur Mathematician Quanta Magazine
- Chromatic Number Definition Examples Video Lesson Transcript Study Com
- A Sudoku Solver Using Graph Coloring Codeproject
- Coloring
- Graph Coloring Business Management Book Chapter Igi Global
Find, Read, And Discover Graph Theory For Coloring, Such Us:
- Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
- Graph Edge Coloring Vizing S Theorem And Goldberg S Conjecture Wiley
- Application Of Graph Coloring In Map Coloring And Gsm Mobile Phone Networks Graph Theory Vertex Graph Theory
- Graph Coloring And Its Applications
- Graph Coloring And Its Applications
If you are looking for Design Coloring Template you've arrived at the perfect location. We have 104 images about design coloring template adding pictures, photos, photographs, wallpapers, and much more. In these page, we also provide number of graphics available. Such as png, jpg, animated gifs, pic art, symbol, black and white, transparent, etc.
6 3 Graph Coloring Problem Backtracking Youtube Design Coloring Template
Graph Coloring Graph Theory Planar Graph Four Color Theorem Mathematics Text Color Graph Of A Function Png Pngwing Design Coloring Template
Point Triangle Mathematics Graph Vertex Graph Theory Graph Coloring Symmetry Graph Of A Function Free Png Pngfuel Design Coloring Template
Graph Coloring And Its Applications Design Coloring Template
Maps Mania Fun With Graph Theory Maps Design Coloring Template
The Four Color Theorem Design Coloring Template
So lets define that and then see prove some facts about it.
Design coloring template. Glossary of graph theory. And were going to call it the basic graph coloring algorithm. And almost you could almost say is a generic approach.
Most of the graph coloring algorithms in practice are based on this approach. The problem is given m colors find a way of coloring the vertices of a graph such that no two adjacent vertices are colored using same color. Matching graph theory in the mathematical discipline of graph theory a matching or independent edge set in a graph is a set of edges without common verticesit may also be an entire graph consisting of edges without common vertices.
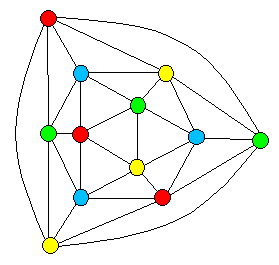
It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. And for our graph g with. A graph coloring for a graph with 6 vertices.
In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color. Discrete mathematics graph theory graph coloring graph coloring. If you want to find out more.
It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. In graph theory graph coloring is a special case of graph labeling. Chromatic number of a graph is the minimum number of colors required to properly color the graph.
Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints. Example 582 if the vertices of a graph represent academic classes and two vertices are adjacent if the corresponding classes have people in common then a coloring of the vertices can be used to schedule class meetings. Vertex coloring is the most common graph coloring problem.
Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints. This number is called the chromatic number and. In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors.
It is impossible to color the graph with 2 colors so the graph has chromatic number 3. Graph coloring has many applications in addition to its intrinsic interest. In graph theory graph coloring is a special case of graph labeling.
And that is probably the most basic graph coloring approach. The assignment of labels or colors to the edges or vertices of a graph. This is called a vertex coloringsimilarly an edge coloring assigns a color to each.
A graph coloring is an assignment of labels called colors to the vertices of a graph such that no two adjacent vertices share the same color. The most common types of graph colorings are edge coloring and vertex coloring.
Introduction To Graph Colouring Youtube Design Coloring Template
Graph Theory Graph Coloring Petersen Graph Chvatal Graph Png Clipart Angle Area Blue Circle Diagram Free Design Coloring Template
Graph Theory Design Coloring Template
Chromatic Number Definition Examples Video Lesson Transcript Study Com Design Coloring Template
More From Design Coloring Template
- Printable New Years Coloring Pages
- Bible Coloring Paint By Number
- Cute Baby Dinosaur Coloring Pages
- Thomas The Train Coloring Pages Online
- Name Coloring Sheets Amy
Incoming Search Terms:
- Acyclic Coloring Graph Coloring Graph Theory Directed Acyclic Graph Png 1200x1200px Graph Coloring Area Color Directed Name Coloring Sheets Amy,
- Ppt Graph Theory And Graph Coloring Lindsay Mullen Powerpoint Presentation Id 2065357 Name Coloring Sheets Amy,
- Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins Name Coloring Sheets Amy,
- Graph Theory Graph Terminologies Planar Graph Graph Colouring Name Coloring Sheets Amy,
- Rainbow Coloring Wikipedia Name Coloring Sheets Amy,
- Applications Of Graph Colouring Youtube Name Coloring Sheets Amy,
