Chromatic Number In Graph Coloring, Eric Sopena Homepage The Incidence Coloring Page

The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color skiena 1990 p.

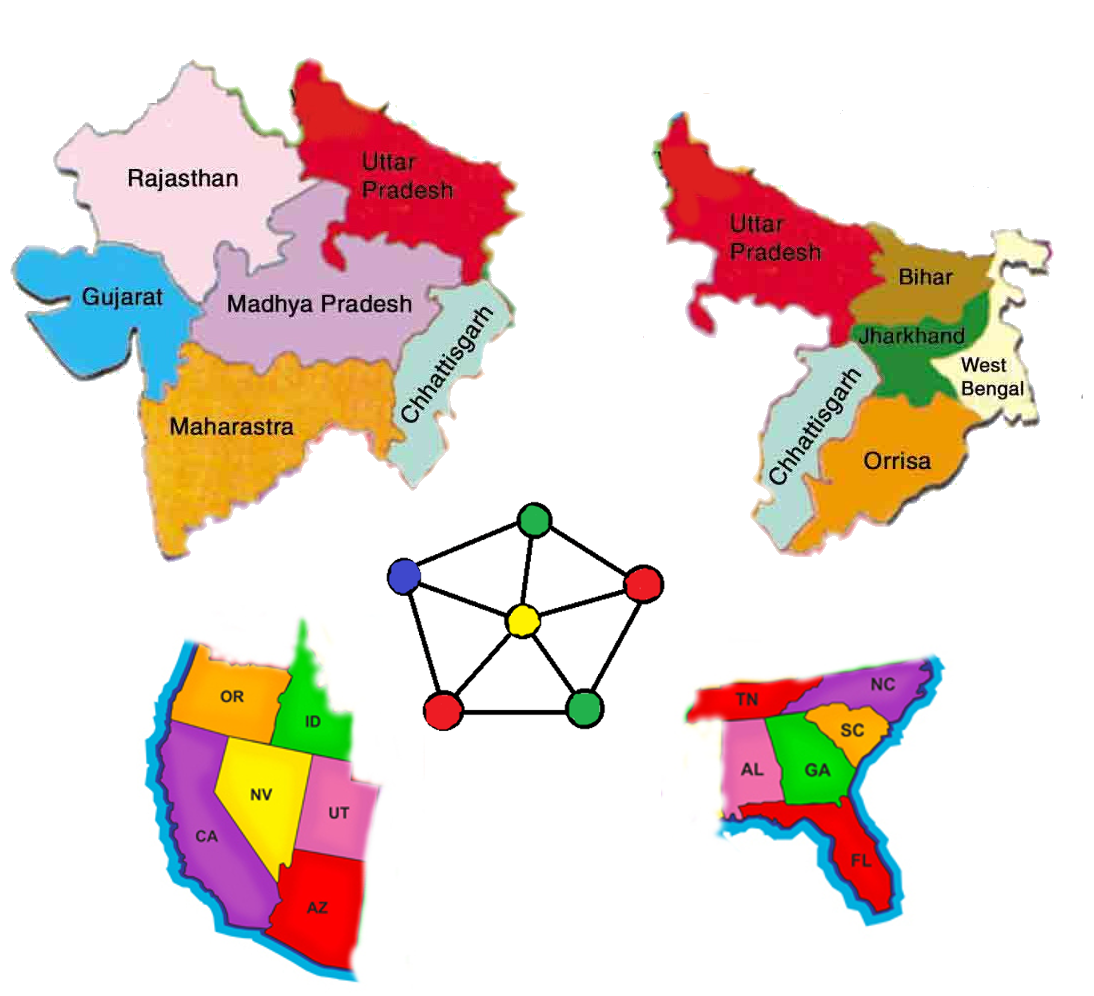
Free printable summer coloring sheets. For example the following can be colored minimum. The other graph coloring problems like edge coloring no vertex is incident to two edges of same color and face coloring geographical map coloring can be transformed into vertex coloring. Bipartite graphs with at least one edge have chromatic number 2 since the two parts are each independent sets and can be colored with a single color.

The chromatic polynomial is a function pg t that counts the number of t colorings of gas the name indicates for a given g the function is indeed a polynomial in tfor the example graph pg t tt 1 2 t 2 and indeed pg 4 72. The chromatic number x g chig x g of a graph g g g is the minimal number of colors for which such an. The chromatic number of a graph is the minimum number of colors needed to produce a proper coloring of a graph.

Chromatic number of a graph is the minimum number of colors required to properly color the graph. Graph coloring is a np complete problem. Hence the chromatic number of k n n.

However a following greedy algorithm is known for finding the chromatic number of any given graph. N1 n2 n2 consider this example with k 4. There exists no efficient algorithm for coloring a graph with minimum number of colors.

Graph coloring is one of the most important concepts in graph theory. Conversely if a graph can be 2 colored it is bipartite since all edges connect vertices of different colors. The chromatic number of kn is.

Hence each vertex requires a new color. Color first vertex with the first color. Applications of graph coloring.

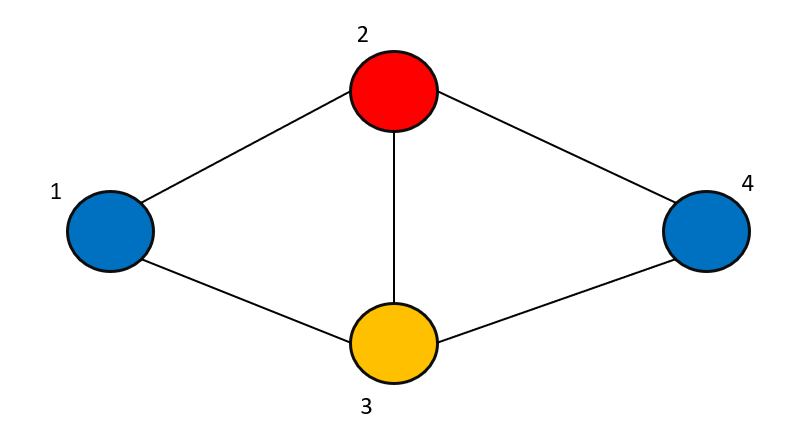
A graph coloring is an assignment of labels called colors to the vertices of a graph such that no two adjacent vertices share the same color. Graph coloring in graph theory graph coloring is a process of assigning colors to the vertices such that no two adjacent vertices get the same color. The chromatic number of a graph is most commonly denoted.

Unfortunately there is no efficient algorithm available for coloring a graph with minimum number of colors as the problem is a known np complete problemthere are approximate algorithms to solve the problem though. It is impossible to color the graph with 2 colors so the graph has chromatic number 3. We introduced graph coloring and applications in previous post.

In our scheduling example the chromatic number of the graph would be the minimum. A graph coloring for a graph with 6 vertices. The smallest number of colors needed to color a graph g is called its chromatic number.

The chromatic polynomial includes at least as much information about the colorability of g as does the chromatic number.