Chromatic Number In Coloring, 2

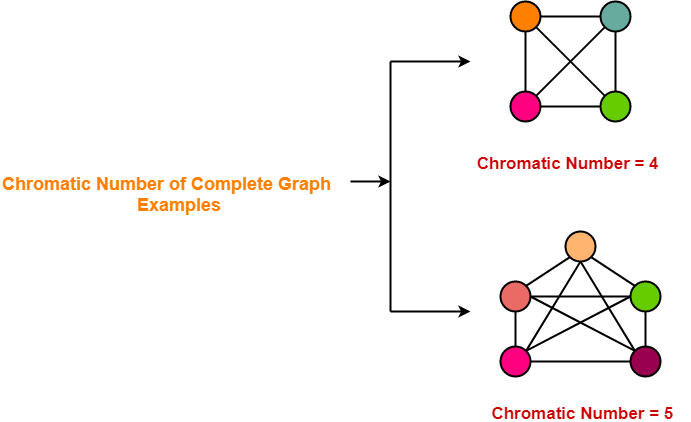
The chromatic number of kn is.

Penguin with santa hat coloring page. The chromatic number of a graph is the minimum number of colors needed to produce a proper coloring of a graph. Graph coloring in graph theory graph coloring is a process of assigning colors to the vertices such that no two adjacent vertices get the same color. Hence the chromatic number of k n n.

Hence each vertex requires a new color. The chromatic number x g chig x g of a graph g g g is the minimal number of colors for which such an. The smallest number of colors needed to color a graph g is called its chromatic number.

Chromatic number of a graph is the minimum number of colors required to properly color the graph. Minimal colorings and chromatic numbers for a sample of graphs are illustrated above. Minimum number of colors required to color the given graph are 3.

Therefore chromatic number of the given graph 3. The other graph coloring problems like edge coloring no vertex is incident to two edges of same color and face coloring geographical map coloring can be transformed into vertex coloring. Graph coloring is one of the most important concepts in graph theory.

This function computes a b coloring with at most k colors that maximizes the number of colors if such a coloring exists. Given a proper coloring of a graph g and a color class c such that none of its vertices have neighbors in all the. In the complete graph each vertex is adjacent to remaining n 1 vertices.

Get more notes and other study material of graph theory. The chromatic polynomial is a function pg t that counts the number of t colorings of gas the name indicates for a given g the function is indeed a polynomial in tfor the example graph pg t tt 1 2 t 2 and indeed pg 4 72. In our scheduling example the chromatic number of the graph would be the minimum.

For example the following can be colored minimum. 210 ie the smallest value of k possible to obtain a k coloring. A graph coloring for a graph with 6 vertices.

A graph coloring is an assignment of labels called colors to the vertices of a graph such that no two adjacent vertices share the same color. It is impossible to color the graph with 2 colors so the graph has chromatic number 3. The chromatic polynomial includes at least as much information about the colorability of g as does the chromatic number.

N1 n2 n2 consider this example with k 4. The chromatic number of a graph g is the smallest number of colors needed to color the vertices of g so that no two adjacent vertices share the same color skiena 1990 p. The given graph may be properly colored using 3 colors as shown below to gain better understanding about how to find chromatic number watch this video lecture.

Applications of graph coloring.